출처 : www.acmicpc.net/problem/17472
17472번: 다리 만들기 2
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
www.acmicpc.net
문제
섬으로 이루어진 나라가 있고, 모든 섬을 다리로 연결하려고 한다. 이 나라의 지도는 N×M 크기의 이차원 격자로 나타낼 수 있고, 격자의 각 칸은 땅이거나 바다이다.
섬은 연결된 땅이 상하좌우로 붙어있는 덩어리를 말하고, 아래 그림은 네 개의 섬으로 이루어진 나라이다. 색칠되어있는 칸은 땅이다.
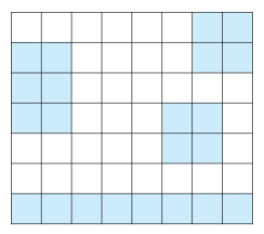
다리는 바다에만 건설할 수 있고, 다리의 길이는 다리가 격자에서 차지하는 칸의 수이다. 다리를 연결해서 모든 섬을 연결하려고 한다. 섬 A에서 다리를 통해 섬 B로 갈 수 있을 때, 섬 A와 B를 연결되었다고 한다. 다리의 양 끝은 섬과 인접한 바다 위에 있어야 하고, 한 다리의 방향이 중간에 바뀌면 안된다. 또, 다리의 길이는 2 이상이어야 한다.
다리의 방향이 중간에 바뀌면 안되기 때문에, 다리의 방향은 가로 또는 세로가 될 수 밖에 없다. 방향이 가로인 다리는 다리의 양 끝이 가로 방향으로 섬과 인접해야 하고, 방향이 세로인 다리는 다리의 양 끝이 세로 방향으로 섬과 인접해야 한다.
섬 A와 B를 연결하는 다리가 중간에 섬 C와 인접한 바다를 지나가는 경우에 섬 C는 A, B와 연결되어있는 것이 아니다.
아래 그림은 섬을 모두 연결하는 올바른 2가지 방법이고, 다리는 회색으로 색칠되어 있다. 섬은 정수, 다리는 알파벳 대문자로 구분했다.

|
다리의 총 길이: 13 D는 2와 4를 연결하는 다리이고, 3과는 연결되어 있지 않다. |
다리의 총 길이: 9 (최소) |
다음은 올바르지 않은 3가지 방법이다
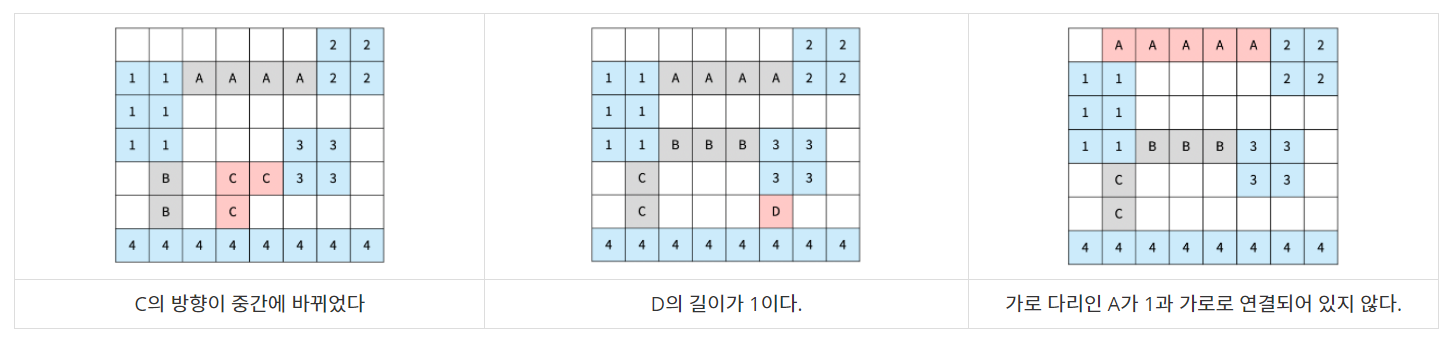
다리가 교차하는 경우가 있을 수도 있다. 교차하는 다리의 길이를 계산할 때는 각 칸이 각 다리의 길이에 모두 포함되어야 한다. 아래는 다리가 교차하는 경우와 기타 다른 경우에 대한 2가지 예시이다.

나라의 정보가 주어졌을 때, 모든 섬을 연결하는 다리 길이의 최솟값을 구해보자.
입력
첫째 줄에 지도의 세로 크기 N과 가로 크기 M이 주어진다. 둘째 줄부터 N개의 줄에 지도의 정보가 주어진다. 각 줄은 M개의 수로 이루어져 있으며, 수는 0 또는 1이다. 0은 바다, 1은 땅을 의미한다.
출력
모든 섬을 연결하는 다리 길이의 최솟값을 출력한다. 모든 섬을 연결하는 것이 불가능하면 -1을 출력한다.
제한
- 1 ≤ N, M ≤ 10
- 3 ≤ N×M ≤ 100
- 2 ≤ 섬의 개수 ≤ 6
풀이
1) 각 섬 숫자 메기기
2) 각 섬에서 다른 번호의 섬까지 거리구하기 - 추후에 크루스칼을 통해 MST 구해야 하므로 from, to, weight 추가
3) 크루스칼 MST 를 사용해 최소연결트리 구하면 된다.
시간이 오래걸린 이유
1) 각 섬에서 번호를 구할 때, 한 방향 탐색을 어떻게 해야할지 어려웠다.
--> for문을 바깥으로 두고, 안에 while ( !queue.isEmpty() ) 형태로 두어서 처리해야 한다.
2) 우선순위 큐를 안쓰고 풀려고 했다. 답은 나온다. 하지만, 중복되는 값들이 매우 많이 저장되는 문제가 발생한다.
--> 우선순위 큐 쓰자
3) 마지막에, 연결된 간선의 개수가 ( 섬의개수 - 1 ) 라면, answer 값을 0으로 초기화 해줬어야 하는데 그 부분때문에 오류가 났다. 다른 이유가 있을 것 같아서 2일에 걸쳐 코드를 처음부터 다시 짰다.
코드
package 알고리즘공부하기;
import java.awt.Point;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class 다리만들기2_17472 {
static int dr[] = { -1, 0, 1, 0 };
static int dc[] = { 0, 1, 0, -1 };
static int N, M; // N : row , M : col
static int[][] map;
static int island_number = 0;
static ArrayList<island> graph = new ArrayList<>();
static int[] parents;
static int answer=0;
static public class island {
int from;
int to;
int count;
public island(int from, int to, int count) {
this.from = from;
this.to = to;
this.count = count;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
M = sc.nextInt();
map = new int[N][M];
// input
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
map[i][j] = sc.nextInt() * (-1); // 섬은 -1로 저장
}
}
// (1) numbering
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
// 섬을 만났을 때
if (map[i][j] == -1) {
island_number++;
numbering(i, j);
}
}
}
// 섬의 개수 만큼 집단 만들자
parents = new int[island_number + 1]; // 1부터 시작할껴 ~
for ( int i=1; i<=island_number; i++) {
parents[i] = i;
}
// test
//print();
// (2) make graph - kruskal Algorithm 사용하자. - 인접한 섬 간의 거리를 구해야해
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
// 처음 부터 돌면서 섬을 만난다면
int from = map[i][j];
if (from != 0) {
// 사방향 직진해보면서 다른 땅만나는지 체크하기
makegraph(i, j, from);
}
}
}
Collections.sort(graph, new Comparator<island>() {
@Override
public int compare(island o1, island o2) {
// TODO Auto-generated method stub
if (o1.count < o2.count) {
return -1;
} else if (o1.count > o2.count) {
return 1;
}
return 0;
}
});
//test
// for( int i=0; i<graph.size(); i++) {
// System.out.println("from : "+ graph.get(i).from + " to : " + graph.get(i).to + " count : " + graph.get(i).count);
// }
// (3) get minimum distance - kruskal - 궁금한거 하나 ! 간선 가중치 같은 애들 중에 최적 어떻게?
kruskal();
System.out.println(answer ==0 ? -1 : answer );
}
private static void kruskal() {
// kruskal based graph.
int cnt =0;
for( int i=0; i< graph.size(); i++) {
// graph 안에 있는 from to 가 서로 union가능하면 합치기
int from = graph.get(i).from;
int to = graph.get(i).to;
if ( findParent(from) != findParent(to)) {
union(from,to);
answer += graph.get(i).count;
cnt ++;
}
// 정점 -1 개 만큼 간선 되면 그만 ~
if ( cnt == island_number-1) {
break;
}
}
if ( cnt != island_number-1) answer =0;
}
private static void union(int from, int to) {
// 부모가 다르다면
int px = findParent(from);
int py = findParent(to);
parents[px] = py;
}
private static int findParent(int from) {
if ( parents[from] == from) {
return from;
}
else {
parents[from] = findParent( parents[from]);
return parents[from];
}
}
private static void makegraph(int r, int c, int from) {
// bfs로 인접한 섬 찾자.
Queue<island> queue = new LinkedList<>();
// from : " r " ---> to : " c "
// count 는 2개 이상 이여야하고, 직진으로 가야한다.
for (int d = 0; d < 4; d++) {
queue.add(new island(r, c, 0)); // 해당 위치부터 시작
int nr = r + dr[d];
int nc = c + dc[d];
// 다음 갈 곳이 바다라면 고고
if (isIn(nr, nc) && map[nr][nc] == 0) {
// 계속 가야해
while (!queue.isEmpty()) {
island cur = queue.poll();
// 한 방향으로 계속 가자
nr = cur.from + dr[d];
nc = cur.to + dc[d];
if (isIn(nr, nc) && map[nr][nc] == 0) { // 바다라면
// 큐에 다음 count 올리고 전진
queue.add(new island(nr, nc, cur.count + 1));
}
// 다음 갈 곳이 다른 섬이라면!?
else if (isIn(nr, nc) && map[nr][nc] != from && cur.count>=2) {
// 카운트는 추가할 필요없이, from to count 를 추가하고
graph.add(new island(from, map[nr][nc], cur.count));
break;
}
}
}
queue.clear();
}
}
private static void print() {
// TODO Auto-generated method stub
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
private static void numbering(int r, int c) {
// TODO Auto-generated method stub
Queue<Point> queue = new LinkedList<>();
queue.add(new Point(r, c)); // 큐에 넣기
map[r][c] = island_number; // 방문 표시 & 숫자 표시
while (!queue.isEmpty()) {
Point Cur = queue.poll();
for (int d = 0; d < 4; d++) {
int nr = Cur.x + dr[d];
int nc = Cur.y + dc[d];
// 맵 안에 있고, 인접한 섬이라면
if (isIn(nr, nc) && map[nr][nc] == -1) {
map[nr][nc] = island_number; // 방문표시하고
queue.add(new Point(nr, nc)); // 큐에넣고 반복하자.
}
}
}
}
private static boolean isIn(int nr, int nc) {
// TODO Auto-generated method stub
if (nr >= 0 && nr < N && nc >= 0 && nc < M)
return true;
return false;
}
}
우선순위 큐를 사용한 코드
package 알고리즘공부하기;
import java.awt.Point;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
public class 다리만들기2_17472_v2 {
static int dr[] = { -1, 0, 1, 0 };
static int dc[] = { 0, 1, 0, -1 };
static int N, M; // N : row , M : col
static int[][] map;
static int island_number = 0;
static PriorityQueue<island> graph = new PriorityQueue<island>();
static int[] parents;
static int answer=0;
static public class island implements Comparable<island> {
int from;
int to;
int count;
public island(int from, int to, int count) {
this.from = from;
this.to = to;
this.count = count;
}
@Override
public int compareTo(island o) {
// TODO Auto-generated method stub
return o.count >= this.count ? -1:1;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
M = sc.nextInt();
map = new int[N][M];
// input
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
map[i][j] = sc.nextInt() * (-1); // 섬은 -1로 저장
}
}
// (1) numbering
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
// 섬을 만났을 때
if (map[i][j] == -1) {
island_number++;
numbering(i, j);
}
}
}
// 섬의 개수 만큼 집단 만들자
parents = new int[island_number + 1]; // 1부터 시작할껴 ~
for ( int i=1; i<=island_number; i++) {
parents[i] = i;
}
// test
//print();
// (2) make graph - kruskal Algorithm 사용하자. - 인접한 섬 간의 거리를 구해야해
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
// 처음 부터 돌면서 섬을 만난다면
int from = map[i][j];
if (from != 0) {
// 사방향 직진해보면서 다른 땅만나는지 체크하기
makegraph(i, j, from);
}
}
}
// Collections.sort(graph, new Comparator<island>() {
//
// @Override
// public int compare(island o1, island o2) {
// // TODO Auto-generated method stub
// if (o1.count < o2.count) {
// return -1;
// } else if (o1.count > o2.count) {
// return 1;
// }
//
// return 0;
// }
//
// });
//test
// for( int i=0; i<graph.size(); i++) {
// island tmp = graph.poll();
// System.out.println("from : "+ tmp.from + " to : " + tmp.to + " count : " + tmp.count);
// }
// (3) get minimum distance - kruskal - 궁금한거 하나 ! 간선 가중치 같은 애들 중에 최적 어떻게?
kruskal();
System.out.println(answer ==0 ? -1 : answer );
}
private static void kruskal() {
// kruskal based graph.
int cnt =0;
for( int i=0; i< graph.size(); i++) {
// graph 안에 있는 from to 가 서로 union가능하면 합치기
island tmp = graph.poll();
int from = tmp.from;
int to = tmp.to;
if ( findParent(from) != findParent(to)) {
union(from,to);
answer += tmp.count;
cnt ++;
}
// 정점 -1 개 만큼 간선 되면 그만 ~
if ( cnt == island_number-1) {
break;
}
}
if ( cnt != island_number-1) answer =0;
}
private static void union(int from, int to) {
// 부모가 다르다면
int px = findParent(from);
int py = findParent(to);
parents[px] = py;
}
private static int findParent(int from) {
if ( parents[from] == from) {
return from;
}
else {
parents[from] = findParent( parents[from]);
return parents[from];
}
}
private static void makegraph(int r, int c, int from) {
// bfs로 인접한 섬 찾자.
Queue<island> queue = new LinkedList<>();
// from : " r " ---> to : " c "
// count 는 2개 이상 이여야하고, 직진으로 가야한다.
for (int d = 0; d < 4; d++) {
queue.add(new island(r, c, 0)); // 해당 위치부터 시작
int nr = r + dr[d];
int nc = c + dc[d];
// 다음 갈 곳이 바다라면 고고
if (isIn(nr, nc) && map[nr][nc] == 0) {
// 계속 가야해
while (!queue.isEmpty()) {
island cur = queue.poll();
// 한 방향으로 계속 가자
nr = cur.from + dr[d];
nc = cur.to + dc[d];
if (isIn(nr, nc) && map[nr][nc] == 0) { // 바다라면
// 큐에 다음 count 올리고 전진
queue.add(new island(nr, nc, cur.count + 1));
}
// 다음 갈 곳이 다른 섬이라면!?
else if (isIn(nr, nc) && map[nr][nc] != from && cur.count>=2) {
// 카운트는 추가할 필요없이, from to count 를 추가하고
graph.add(new island(from, map[nr][nc], cur.count));
break;
}
}
}
queue.clear();
}
}
private static void print() {
// TODO Auto-generated method stub
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
private static void numbering(int r, int c) {
// TODO Auto-generated method stub
Queue<Point> queue = new LinkedList<>();
queue.add(new Point(r, c)); // 큐에 넣기
map[r][c] = island_number; // 방문 표시 & 숫자 표시
while (!queue.isEmpty()) {
Point Cur = queue.poll();
for (int d = 0; d < 4; d++) {
int nr = Cur.x + dr[d];
int nc = Cur.y + dc[d];
// 맵 안에 있고, 인접한 섬이라면
if (isIn(nr, nc) && map[nr][nc] == -1) {
map[nr][nc] = island_number; // 방문표시하고
queue.add(new Point(nr, nc)); // 큐에넣고 반복하자.
}
}
}
}
private static boolean isIn(int nr, int nc) {
// TODO Auto-generated method stub
if (nr >= 0 && nr < N && nc >= 0 && nc < M)
return true;
return false;
}
}
'알고리즘' 카테고리의 다른 글
| [백준] 보물섬 2589 [JAVA] (0) | 2020.09.29 |
|---|---|
| [백준] 벌집 2292 [JAVA] (0) | 2020.09.29 |
| [백준] 색종이 2563 JAVA (0) | 2020.09.28 |
| [백준] 수열 2491 [JAVA] (0) | 2020.09.26 |
| [백준] 스위치 켜고 끄기 1244 [JAVA] (0) | 2020.09.25 |


